
 | |
|
Слаботочка Книги Здесь {q{t) = {ехр(1г; лгО ехр(ш 1<), 2, exp(ifit), exp(itivO} - матрица-строка; /)/ = {ii{v-n), ii{v!\i)}t - вектор, компоненты которого представляют комплексные амплитуды токов на /-М НЭ {1-м входе ЛМ); Ж/ - оператор, описывающий связь между током и напряжением на входе /-ГО НЭ; {Z}/p = diag{Z/p(t) Ar), zip{v-i), ziplVo), zip{vi), zip{vi\i)} - диагональная матрица; м - число частных НМ; ei{t) - величина источника ЭДС 1-го входа ЛМ, эквивалентного источникам внешнего возбуждения АНЭ, пересчитанным к сечениям а-а ЛМ; Система уравнений (10.16) полностью эквивалентна системе (10.13), однако в (10.16) под знаком оператора Ш явно выделено слагаемое м {q{t){z}ipi)p, которое описывает Р=1 vi связь между НЭ на основной частоте и частотах гармоник через ЛМ, так как внутри НМ связи между отдельными НЭ нет. Степень связи определяется как элементами матриц {Z}/p, (/ ф р), так и величиной токов на клеммах частных НМ 1)р, V/ ф р. Вследствие этого, если известно приближенное ре- шение (10.16) в виде векторов i)) , V/ = 1,М, то следующее {к 4- 1)-е при- ближение /)/ можно определить из решения м независимых уравнений {q{t)i)\++ri{{q{t){z}ui)\+4 -a\t)+€i{t)} = 0; V/ = I7M; ott, (10.17) rea4\t)=£{q{t){zulp. p=i Решение каждого из уравнений (10.17) на одной из итераций верхне-го уровня, т.е. определение I)] при постоянном значении к, выполняемое с применением итерационных процедур, составляет сущность итерационного процесса нижнего уровня. В свою очередь, нахождение последовательности {к - 0,1...) образует итерационный процесс верхнего уровня. При этом, если итерационный процесс (10.17) сходится, то он сходится к точному решению системы (10.16). Использование идеи декомпозиции позволяет при одинаковой точности получаемых результатов анализировать схемы, содержащие как минимум в 2-3 раза больше НЭ, чем это возможно при применении одноуровневых итерационных методов. Описываемый алгоритм открывает дополнительные возможности для дальнейшего увеличения эффективности вычислительного процесса. Во-первых, для ряда анализируемых АНЭ (в частности, для АФАР с идентичными модулями) очень часто оказывается, что несколько из уравнений (10.17) совпадают друг с другом. В этом случае достаточно решить только одно из уравнений и сократить время итераций верхнего уровня. Во-вторых, как правило, степень связи НЭ через линейный многополюсник оказывается различной. При этом возможна ситуация, когда из некоторых уравнений, решаемых на нижнем уровне итерационного процесса, величина aef{t) незначительно отличается от ai\{t), т.е. < 1. Вместо решения /-го уровня (10.17) на данном этапе итераций верхнего уровня достаточно воспользоваться решением этого уравнения на предыдущем этапе. Тем самым уве.личивает-ся общее быстродействие алгоритма за 10.4.3 Методы решения уравнений состояния счет сокращения числа уравнений, решаемых на верхнем уровне итерационного процесса. Еще одна возможность увеличения быстродействия алгоритма состоит в том, что не имеет смысла решать уравнение (10.17) на нижнем уровне итерации с точностью, значительно превышающей точность текущей итерации верхнего уровня. Обычно необходимо, чтобы точность итерационных процессов нижнего уровня несколько превышала точность текущей итерации верхнего уровня. Это приводит к сокращению числа итераций нижнего уровня и, как результат, к сокращению общего числа вычислений. Иногда решение системы уравнений (10.16) можно упростить, используя специфические свойства матрицы линейного многополюсника АНЭ и свойства системы источников возбуждения. Особенно заметное упрощение уравнений состояния можно получить в следующих случаях: а) при анализе кольцевых ФАР с НЭ и приемно-выпрямительных элементов ректенных систем с многофазными схемами выпрямления, т.е. когда матрица ЛМ является блочно-цирку.дянтной, а внешнее воздействие представимо симметричной многофазной системой источников; б) при анализе линейных бесконечных ФАР, каждый модуль которых, в свою очередь, является антенной с НМ. В этом случае матрица ЛМ яв.яяется бесконечно мерной блочно-теплицевой матрицей, а внешнее воздействие - периодическим; в) при анализе плоских бесконечных ФАР, каждый модуль которых - антенна с нелинейными многополюсником, т.е. когда матрица ЛМ является бесконечно мерной блочно-теплицевой, а внешнее воздействие представимо системой источников с двойной периодичностью. Рассмотрим каждый из перечи-с.ченных выше случаев. Случай а. Так как матрица Qqq(u;) является симметричной блоч-но-циркулянтной матрицей, то и матрица Zaa(w) будет обладать такими же свойствами Zk,i{uj) = Zjt ,(a;); Zfc /(u;) = ZM-\k-i\{<)- (10.18) Здесь Zjt /(a;) -блок матрицы ZQcr(a;), описывающий взаимодействие между группами входов, с которыми соединяются соответственно -й и /-Й НМ; Zj{lj) - Z ;j(a;) - элементы матричной последовательности первой строки блоков матрицы Zcra(), т.е. {Zo(u.-),Zi(a;),...,ZM-i(a;)}= (10.19) = {Zo,o(w), Zo,i(a;),..., Zo,m-i()}; М - число НМ в схеме АНЭ. Предполагается, что АНЭ содержит идентичные нелинейные 2т-по.чюсники (рис. 10.13,а), каждый из которых описывается зависимостью (10.12а). Обозначим через £(t)) вектор размерности т, элементами которого являются ЭДС холостого хода группы входов, соединяемых с к-ш нелинейным элементом .r(o) = {4l(o.42W, ,L(m (10.20) где т -операция транспонирования. Если внешнее воздействие АНЭ является периодическим и при этом система источников ЭДС, приведенных к сечениям а-а ЛМ, является симметричной системой, т.е. (t)) = £°(t+ -bfcA)) (здесь At - 27г/(а;оМ)), то вектор комплексных амплитуд токов -й группы входов ЛМ можно выразить через вектор токов входов с нулевым номером Ап(о)) = й(па;о))ехр(тЫоАО = = й(па;о)) ехр(127гг71/М), (10.21) 1 ... m 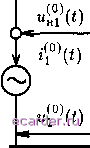
:(М-1) (M-1) 1 ЛМ-1) ei-\t) (M-i) V- Aoai) Рис. io.i3,aj a систему уравнений состояния записать в виде 6nI{nujQ))exp{inujQt)+ +Ш[ 6пЦпшо)1{пи;о))х n = -N xexp(inLJot)-f = 0; OtT. (10.22) Здесь Z{nuJo)= г;(пшо)ехр(127Гп М). /=о (10.23) Таким образом, при оговоренных вначале предположениях относительно матрицы ЛМ и системы источников возбуждения определение переменных состояния для исходной схемы (рис. 10.13,fl) сводится к определению переменных состояния из уравнения (10.22) только для ячейки с нулевым номером и последующим определением для остальных ячеек из соотношения (10.21). Сравнивая (10.22) и (10.13), видим, что система уравнений (10.22) описывает некоторую эквивалентную 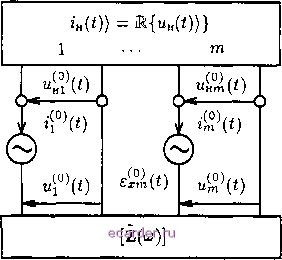 Рис. 10.13,5) АНЭ (рис. 10.13,5), состоящую из одного нелинейного 2т-полюсника, описываемого вольт-амперной характеристикой вида (10.12а), и одного ЛМ, матрица сопротивлений которого определена на частотах всех гармоник и равна 7i{nujQ). Случай б. Определение переменных состояния также сводится к решению уравнения (10.22), так как матрица собственных и взаимных сопротивлений ЛМ является бесконечномерной теплицевой матрицей, блоки которой Zk,i{uj), описывающие взаимодействие между к-м и /-М нелинейными 2т-полюсниками, удовлетворяют со- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 [74] 75 76 77 78 79 80 81 82 83 84 |
|||||||||||||||||||||||||