Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

Решаем (2.4J методом медленно меняющихся амплитуд, используя процедуру частичного укорачивания, для чего раскладываем x{t) на квадратурные составляющие:

X (/) =а (t) sin aot-b (/) cos coo. (2.7)

Опуская промежуточные выкладки, сразу запишем укороченные уравнения для переменных а и &:

da/dt=-b{i)а-\-те(i) cos ио/;

dbldt=-b(0,6+сйоб (О sin соо. \2Щ

Система (2.8) имеет известное решение [57]

(j)=co exp - jS(z)iz jexpj J 8 (z) izj е (r/)X

-GO -00

(2.9)

Видоизменим (2.9): внесем внешнюю экспоненту под знак интеграла

С). . je.p{ ja(.,..).w(--)*(2..0)

и проведем преобразование t t.

J 8 (z) dz= - J 8 (z) t/z - J 8 (z) - f 8 (z) dz.

у V и h

В итоге вместо (2.9) получаем

5(z)rfz

/г, (0 = ехр Кс = ехр

,(0 = expj -b{z)dz

(2.12)

(2.13)

(2.14) 35

ц -обычно малая величина. По установившейся терминологии Кс называется коэффициентом усиления за счет сверхрегенерации [И];

Искомое решение получаем после подстановки (2.11) в (2.7):

x{t) = h,{t)<o, sinw,t h,{t)KtB{t) COS w,tdt -

- cos j A, (t) Ks (t) sin wjdt

-(2.15)

Амплитуда A{t\ и фаза 113(0. соответствующие формуле (2.3), равны:

(2.16) (2.17)

A{t) = Va{t)-i-bt) ;

Заметим, что анализ выражения (2.15) дажепри гармоническом сигнале e,{t) достаточно труден. Это связано с относительной сложностью функций Ai,2(0 (рис. 2.2,

Упростим (укоротим) указанные функции, допуская некоторую погрешность в решении д;(0. Перед этим отметим два условия, которые характеризуют практическое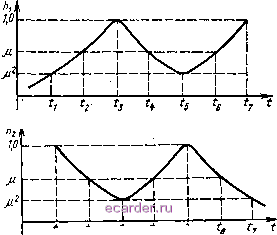

, г Ч Ч S Рис. 2.2. Функции hi,i{t)

й<М10льзование СР. В реальных устройствах CP ставятся в режимы,с большимусилением Кс (как правило, /Сс>10). Кроме того, обычно выполняется неравенство

где tm, tn - любые точки, лежащие одновременно справа или слева от интервала (2 4)-

Неравенство (2.18) означает, что средняя мощность, отдаваемая источником &{t) на интервале (2- 4), не меньше, чем деленная на Кс аналогичная мощность вне данного интервала.

Действительно, СР применяют для усиления весьма слабых сигналов, мощность которых соизмерима с мощностью внутренних шумов или несколько превышает их (обычно не больше, чем на один порядок). Поскольку внутренние шумы СР являются стационарными случай ными процессами, а г{t) учитывает как внешние сигналы, так и внутренние шумы, неравенство (2.18) имеет большую степень достоверности даже в самом неблагоприятном случае, когда импульсный сигнал приходит в момент времени вне интервала (2 . 4)

Отмеченные условия дают возможность ограничиться воздействиями, которые обеспечивают выполнение неравенства (2.18), и, допуская при вычислениях (\ аб-

\b(t)J

солютную погрешность i/ \ заменить в (2.15) функ-ции /i j(<) более простыми, укороченными, функциями

Я.(/) = 0, t,>t>t,;

(2.19)

HAt) = h,{t). t,<t<t,;

для различных применяемых на практике напряжений суперизации - прямоугольного, пилообразного, синусоидального и т. п. Замену функций hi,2{t) их укороченными аналогами H\,2{t) по формулам (2.19) назовем ц-при-ближением.

1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82