Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

Когда точность (х-приближения оказываетсй недостаточной {Кс мало), можно проводить анализ в рамках р,2-приближения, для чего укороченные функции Hi,2{t) определяются следующим образом:

H,{t)K{t), t,<t<t,-

я. (0 = 0. t,>t>t,; H,{t) = hM t,<t<t,; HAt) = 0, t,>t>t,. Укороченные функции Hi,2{t) для р,-приближения изображены на рис. 2.3,а, б. Если Cc>10 верхняя граница погрешности ц=3,3-\0~.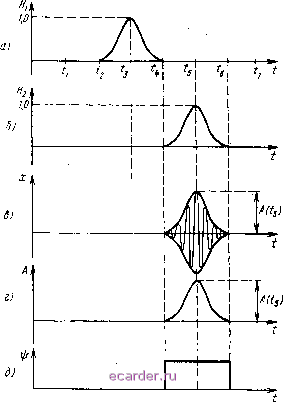

Рис. 2.3. Укороченные функции 1,2(0 i- б), вспын1ка колебаний на выходе CP (в), ее огибающая (г) и фаза заполнения (д)

Подставляя 1[2.19) в (2.11) и (2.15), получаем:

( I ) ад it) J я. it) s (О (; dt; (2.20)

л (О = а (О sin - 6 () cos (ОJ =

sintoi

COS mJd -

- COSm H,{t) sit) sin iojdt

(2.21)

Эти выражения показывают, что процесс л;() в рамках р,-приближения существует лишь на интервале (4 ... б) (рис. 2.3,в) и представляет собой радиоимпульс, у которого огибающая А it) с точностью до постоянного множителя повторяет функцию Яг (О (рис. 2.3,г), а фаза заполнения т); постоянна (рис. 2.3,), причем внешнее воздействие б(0 влияет только на амплитуду А its) вспышки и значение т);. Указанное свойство следует выделить особо, так как оно позволяет-при заданных частоте о и законе суперизации 5(0 форму огибающей выходного процесса определять независимо от сигнала e{t), а действие сигнала оценивать, вычисляя лишь две величины: А its) и ij).

Поскольку однократный запуск СР является частным случаем многократных некогерентных запусков, последние описываются соотношениями, непосредственно вытекающими из (2.20) и (2.21):

(М/СЛЛ-яП) . J Я.(-яГ,)е(<)Х

>/cosV\ 2.22)

xit) = K,HAt-nT,)< ,

sinV 1 HAt-nT,)Bit)X

X COS wjdt - COS f H,{t~ tiT) 8 {t) sin wtdt

(2.23)

где Mc=4i-tt\ n-Q, 1, 2, ... - номер запуска; Гс -период суперизации (период запусков). Некогерентность (независимость) запусков будет иметь место при Гс (<7...i).

Укажем на еще одно эквивалентное условие некогерентности. Для этого вычислим в пределах одного периода суперизации площади 5 и S+ (5 -площадь, ограниченная осью времени и кривой ,б (О <0; S+ -площадь, ограниченная осью врелеки и кривой b{t)>0). Некогерентность будет иметь место, если S+>S .

Схемы, реализующие преобразования (2.21) и (2.23), показаны на рис. 2.4. Решения (2.21), (2.23), а также

fi/tlCOSQJgt

к с М

H,(t}SLno.\t

\-HJt)cosco t

£(t)-

r-*}-* ujj...dt кй)-I

H/t-nTJsinu)J\

шо/... dt

t-utr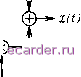

Рис. 2.4. Математические модели CP в некогереитном режиме при однократном (в) и многократном (б) запусках

схемы позволяют легко сравнивать CP с другими устройствами обработки сигналов, находить реакцию CP на случайные и детерминированные воздействия, синтезировать на основе CP локационные, связные и другие системы с высокой помехоустойчивостью. Аналогичные решения и соответствующие им схемы будут найдены (в тех случаях, когда это ие будет связано с большими математическими трудностями) и для параметрических СР.

1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82