
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 по Гауссовскому закону, причем острота кривых определяется значениями коэффициентов Ki,2- Для облегчения расчетов и определения границ режимов удобно ввести в рассмотрение dp -затухание регенерированного контура (т. е. среднее значение d{t)) и полосу пропускания регенерированного контура Пр= -dpfo. Обычно входной (нерегенерированный) контур CP на СВЧ обладает широкой полосой пропускания По, поэтому полоса CP Яср и тем более полоса регенерированного контура Пр всегда меньше По (рис. 3.1). Вооб- 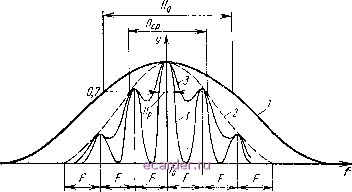 Рис, 3.1. Амплитудно-частотные характеристики: / - нерегенерированного контура; 2 - CP в некогерентном режиме (и огибающая АЧХ в когерентном режиме); 3 - CP в когерентном режиме ще же говоря, как отмечалось еще в [88], понятие полосы пропускания CP как системы с переменными параметрами нуждается в уточнении, поскольку в CP происходит преобразование входной частоты в линейчатый спектр на выходе и, наоборот одной частоте на выходе соответствует набор (гребенка) дискретных частот на входе. Поэтому под полосой CP (на уровне 0,7) условимся понимать полосу, соответствующую гладкой кри-. вой при некогерентном режиме или огибающей максимумов при когерентном режиме (см. рис. 3.1). Заметим, что эквивалентные (шумовые) полосы CP в некогерентном и когерентном режимах оказываются одного порядка; обычно Пср(2,5 ... 3,2)F в некогерентном режиме и Пср(4 ... 5) Пр в когерентном режиме. Определим параметры вспышек CP при некоторых детерминированных воздействиях. Воздействие одним гармоническим сигналом. Пусть s(/)=:4sin[K-Aco) + 4.J. (3.2) Подставляя (3.2) в (2.20) и учитывая (2.16), (2.17) и (3.1), для однократного запуска находим: Х(0--Л(дЯ,(0сО8 (со/+ф); A(t,) = KA, К, = К,К,; (3.3) 4 = tc+arg5.(jA )=:4.,-A<. (3.4) Суммарный коэффициент усиления является произведением коэффициента усиления за счет сверхрегенерации Кс и множителя Кя, определяемого формулой К, = \8А]Щ\ \H,{t)dt. (3.5) ЕслиАю = 0, = о=4- о \At)dt, ФФс (3.6) - со К,= Л(;,)/Л,:=--7С Л,. (3.7) Множитель К-а называется коэффициентом накопления. Он показывает, во сколько раз амплитуда Л (5) вспышки СР увеличена в сравнении с амплитудой Лс только за счет энергии, внесенной в контур источником внешнего сигнала на интервале [t ... ti). Воздействие двумя гармоническими сигналами. Положим, что e(0=ei(/)+e2(0: S, (0=Л Sin[( - Д .)/ + ф; s,(0 = 4.sin[(a) - AcoJ + 4;J. Поскольку система линейна, находим ее реакцию на £i(0 и е2(/) отдельно и затем результаты складываем,: X (t) = К,К М, (/) [Л IS, (jAo)J I cos Ы + 4-0 + + Л,5Л]Д .)со8( /+ф]; (3.8) b.cc + argSJjAco. ). (3.9) При многократных независимых запусках с частотой F получаем последовательность вспышек с амплитудной модуляцией, частота которой определяется произвсдени- ем F на дробную часть отношения A(ai-А(й2/2яР, а глубина оценивается формулами t.l/at)l с.15.0Дш.)1<Л.5,0Дсо,); (3.10) = 1 S, (jA<o,) К Л I S, (jA >,) . Воздействие узкополосным сигналом. Полагаем, что сигнал е(0 имеет достаточно малую ширину спектра (в несколько раз меньшую полосы пропускания Пор). При этом амплитуда Лс(0 и фаза ч)с(0 сигнала е (О - Л, (0. sin [(со - Д<о) + (0] (3.11) - медленно меняющиеся функции. Следовательно, на интервале (t ... ti) их можно отождествлять с постоянными величинами, равными соответственно Ac{h) И с(з), и узкополосное воздействие анализировать так же, как гармоническое с амплитудой Лс(4) и фазой А (t) = Л, (з) (t) 15, (jAo)) I; (3.12) <l = tcW + arg5,(jA ); (3.13) A{t,)=:A,{QK,K,\SAi4\- (3-14) Соотношение (3.14) показывает, что амплитуда вспышки Л (ts) с точностью до постоянного множителя повторяет амплитуду сигнала Л о (О в момент з- Другими словами, CP осуществляет считывание (дискретизацию) функции Лс(0 в точке и переносит значение Лс(з) на амплитуду вспышки с усилением /CcKho1s,(jA(o)1. Раскрывая argSi(/Aft)) в (3.13), находим Ц==сЩ-Шз. (3.15) Если сигнал (3.11) записать в форме е(0=Лс(051п M-fфc(0]. где фо=-А(й/+о(0 выражение (3.13) с учетом (3.15) можно представить в виде г))=Фс(з). (3.16) Таким образом, фаза заполнения вспышки повторяет значение фазы фс(0 в точке h, следовательно, по отношению к узкополосному воздействию CP является дис- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |