Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

в аргументе функции Бесселя d-p на do. Поскольку первая замена приводит к уменьшению Кр всего примерно на два порядка, а вторая -к увеличению затухания на несколько порядков, условие некогерентности автоматически выполняется.

3.2. Расчет параметрических сверхрегенераторов

В параметрических СР, в некогерентном режиме, которые описываются уравнениями (2.29), (2.42) и (2.43), выходной процесс определяется формулой (2.37), где фигурируют характеристики Hi,2{t). Эти функции можно найти из соотношений (2.12), (2.13) и (2.19), если предварительно определен закон суперизации 6(0 в (2.33). Спектральные характеристики 51,2(jАсо) получим из (3.1), полагая, что Асй=сос-v. Временные H\2{t) и модули спектральных Si,2(jAco) характеристик для прямоугольного, пилообразного и синусоидального напряжений суперизации при некогереитном режиме приведены в табл. 3.1.

Частотные характеристики параметрических СР для любого режима довольно громоздки, и их целесообразно рассчитывать с помощью ЭВМ. Это сделано в работе [26], где получены частотные характеристики для параметрического СР при Пр< (рис. 3.4) и np>f (рис. 3.5). На рис. 3.4,а кривая 1 -АЧХ параметрического усилителя с усилением, равным усилению параметрического СР; кривая 2 - зависимость уровня сигнала частоты сос на выходе от частоты входного сигнала сос. Как видим, ширина полосы пропускания кривой 2 даже для основного максимума значительно шире, чем у кривой 1. Кривые 3 и 4 являются зависимостью уровня сигналов на выходе частот сос-й и сос-2Q соответственно от частоты входного сигнала сос. Эти две кривые асимметричны относительно половины частоты накачки. Например, если сигнал будет поступать на частоте cuc=v-f-Q, то на центральной частоте v (кривая 3) можно отфильтровать еще высокий уровень сигнала. Но если сигнал подавать на coc=v, то на частоте v-Q может быть снят уже более слабый сигнал. Зато при подаче сигнала на частоте соо= =v-f-2Q выходное напряжение на частоте v-f-Q оказывается большим.

Кривая 5 представляет собой АЧХ регенерированного контура до включения напряжения суперизации.

6* 83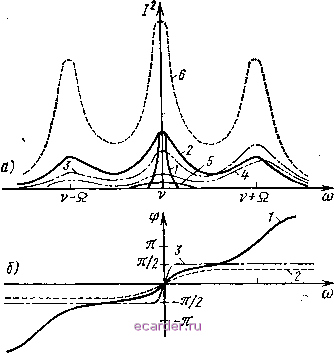

Рис. 3.4. Характеристики параметрического CP для np = 0,2F: а - амплитудно-частотные; 6 - фазочастотные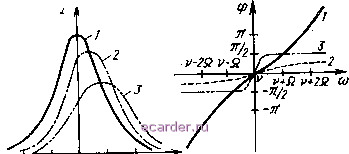

Рис. 3.5. Характеристики параметрического CP для Пр = 4Р.-а - амплитудно-частотные; б - фазочастотные

и усиление, и полоса в этом случае значительно меньше, чем при сверхрегенеративном режиме. Кривая 6 соответствует случаю, когда отфильтровывается не одна частота на выходе, а весь отклик СР на сигнал, поступающий на вход с частотой Мс- Как видно из рисунка, уровень сигнала на выходе при этом в несколько раз выше, чем при приеме одной частоты. Такой же вывод был получен аналитически при сопоставлении формул (3.34) и (3.36).

На рис. 3.5,0 кривая 1 представляет собой АЧХ для сигнального компонента, т. е. зависимость уровня сигнала <ос на выходе от частоты входного сигнала с , кривая 2 -зависимость первого компонента сос-й, а кривая 3 - второго компонента сос-2Q от частоты сигнала Мс. В отличие от кривых на рис. 3.4,а, АЧХ на рис. 3.5,а гладкие. Фазовые характеристики (см. рис. 3.4,а и 3.5,а) имеют удовлетворительную линейность, особенно при Пр>Л Поэтому можно считать, что параметрический СР не вносит существенных фазовых искажений.

Рассмотрим теперь результаты некоторых детермини.-рованных воздействий на параметрический СР.

Воздействие одним гармоническим сигналом. Пусть

е(0=-Лс8ш (vi-А(й+г)сУ, (3.38)

где A(B=v-сос; с - частота сигнала.

Подставляя (3.38) в (2.36) и учитывая \ЗЛ), получаем

x(t)=AcKnKcH2(t) cos (v+фо). (3.39)

/Сн=-Д:но5,(]Дсо) I cos [грс-o+argSi(jA(D)]

(3.40)

- коэффициент накопления;

н,- ]H,{t)dt~ (3.41)

- коэффициент накопления при Дсй=0 и фс=фо. Амплитуда A{ts) и фаза вспышки в соответствии

с формулами (2.37) и (2.38) определяются выражениями:

A{h)=A,\KAKc; (3.42)

cos sgn COS [фс-фо-f arg Si (jДсо) ]. (3.43)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82