Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

колебательной системой, он не усиливается, как это имеет место в классичесйом CP, а обеспечивает качественные либо количественные изменения поведения автоколебательной системы в зависимости от текущей фазы, отсчитываемой относительно фазы опорного напряжения. Указанные изменения в ФСР проявляются в появлении вспышек генерации, следующих с разностной частотой между частотами принимаемого и опорного сигналов, в ФСРДС - в изменении амплитуды вспышек генерации с той же разностной частотой. Это означает, что в обычные параметры, характеризующие классический CP, необходимо ввести некоторые коррективы, учитывающие отмеченные особенности фазовых СР.

Основными параметрами и характеристиками, определяющими свойства ФСР, являются коэффициент усиления и частотная характеристика.

Под коэффициентом усиления ФСР будем понимать отношение амплитуды переменной составляющей выходного сигнала Umax (в ФСР - амплитуды вспышек, в ФСРДС - изменения амплитуды вспышек генерации) к амплитуде сигнала Ep. Заметим, что в этом определении есть известная условность. Дело в том, что t/max определяется напряжением на колебательном контуре, вызванном шумами, а не напряжением сигнала, так как в фазовых CP входной сигнал выполняет функции напряжения суперизации, а усиливаются в обычном понимании лишь шумы контура и резонансного усилителя. Поэтому амплитуда вспышки колебаний на контуре, обычно близкая к напряжению насыщения усилительного прибора, формально не может рассматриваться как усиленный сигнал. Однако, поскольку сигнал Ер также определяет амплитуду вспышек, можно с учетом сделанных замечаний для ФСР записать

y=f/ o/£n.p=f/max/Enp, (3.72)

где U,YsJQKJ<py - среднеквадратическое значение

шума на выходе (амплитуда выходного сигнала ФСР); So -спектральная плотность . шумов контура и резонансного усилителя, пересчитанных на вход РУ; Ks, Пш -коэффициент усиления и шумовая полоса регенерированного контура CP, напряжение суперизации которого соответствует входному сигналу ФСР; /Сру - коэффициент усиления резонансного усилителя.

Для ФСРДС полезным эффектом является приращение амплитуды вспыщек, пропорциональное приращению коэффициента усиления Аг- Поэтому коэффициент усиления ФСРДС

= иАК,К!Е, = Цпах/пР (3-73)

где Uysn, .

Значения Ks, A.Ks, Пш, фигурирующие в (3.72) и (3.73), можно рассчитать по методике, изложенной в § 2.4 и 3.1.

Частотная характеристика ФСР представляет собой зависимость коэффициента усиления от частоты сигнала сос. Так как частота сигнала и частота суперизации Q связаны соотнощением Q-toc-Юоп, частотную характеристику ФСР можно трактовать как зависимость Ку от частоты суперизации Й.

Частотные характеристики Kj{Q) ФСР и ФСРДС можно рассчитать на основании (3.72) и (3.73) соответственно, если раскрыть зависимость Ks. и AKs для различных напряжений суперизации. Для ее определения удобно использовать соотнощение вида

F{x) = e -lx. (3.74)

одинаковое для различных типов ФСР и напряжений суперизации. В (3.74) х - некоторая переменная, линейно зависящая от частоты суперизации Q и различ- f ная для разных законов суперизации; F{x) - функция, пропорциональная /Су(Й).

Особенностью зависимости F{x) (3.74) (рис. 3.17) является ограничение области изменения х снизу {х>Хо). Это означает, что ФСР имеет нерабочую область, в пределах которой нарушается условие когерентности режима, а на выходе ФСР формируются случайные вспышки генерации. При уменьшении принимаемого сигнала нерабочая область л; увеличивается до бесконечности, когда ФСР становится неработоспособным. По мере

, Нера5очай область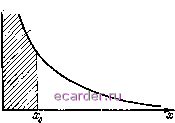

Рис. 3.17. Частотная характеристика ФСР при прямоугольном напряжении суперизации

увеличения амплитуды принимаемого сйгйала нерабочая область уменьп1ается, стремясь к некоторому предельному значению хр.

Выражения F{x), х, Хщ, и условия достижения Хщ, для различных законов изменения фазы приведены в табл. 3.2, где {/щ, = [/5 Пш/(ру. Используя данные

таблицы, можно найти /Су(Й) для ФСР.

Частотные характеристики ФСРДС при различных законах суперизации определяются соотношением

(3.75)

Уд max - Р

где /(y(Q) -частотная характеристика ФСР, которую можно рассчитать в соответствии с формулами табл. 3.2, если положить в них

/(8Ш¥д. = /(со8д, = Д6 = 8, = /(; (3.76)

Т а б л и ц и 3.2

Форма напряжения суперизации

F (х)

Условия до-

стижения x,

Прямоугольная

Симметричная пилообраз-ня

Синусоидальная

8р Чи. Х(А8 -28) = /2ДЙ

Х(К 81п д,-

2л(Д8 -28)2

(К sin <рд, + + 23уд,)9/4, (рд, = агссо8 28/7С

л: cos .рд2 > >23

Д328

л:>28

Р 8Д

8р Д8

°Р

ёг -предельное отрицательное значение дополнительной функции суперизации, удовлетворяющее неравенству б25срдп1ах/2; Й = Од; Йд - частота дополнительной суперизации.

Анализируя (3.76) и данные табл. 3.2, можно заключить, что при выборе частоты дополнительной суперизации, равной Йд=5фдгаах, И ПОЛОСЫ пропускания, равной 112

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82