
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 [42] 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 отклик на внешнее воздействие и шум на выходе определится формулой (4.6) РазделивJ4.6) на среднеквадратическое значение шума на входе £ш = 5вхПрш, найдем коэффициент усиления по шуму /(m2=/2o(2p)moQ2p/Q2e . (4.7) Относя (4.7) к (3.36) -усилению сигнала для этого случая, найдем коэффициент шума Шер=/Сш2/Ср2=Шо/о (2р) 2о (Р) -=рШо. Как видим, это выражение не отличается от (4.5). Это вполне естественно: 1 I в этом случае и сигнал, и шум увеличатся в jt? раз. 1 . I I к1 1,. . к. gj......I .1
fg-2F fg-F fo VF fo*-2F f a) Рис. 4.1. Спектры сигналов на входе и выходе CP: а - пни сигнале па частоте настройки; б, в - при расстройке; г - астотпая характеристика фильтра иа вы-.\оде CP Рис. 4.2. Преобразование шумов в CP: а - шумы иа частотах fn±kF; б - шумы па основной частоте так что отношение сигнала к шуму не должно измениться. На рис. 4.3 показана зависимость р от р. Поскольку обычно на практике р=4 ... 5, коэффициент шума увеличится на 4 ... 6 дБ. Естественно, что при этом уменьшается и пороговая чувствительность, которая должна вычисляться по формуле гпор (4.8) где /а - относительная шумовая температура. Заметим, что при измерении коэффициента шума с помощью шумового генератора его увеличение не обнаруживается, так как в этом случае компоненты шума присутствуют во всей полосе нерегенерированного контура, т. е. тоже увеличиваются в р раз. Если а~1, получаем приближенное значение пороговой чувствительности j пор 7Прш/5Шо. Поскольку /)Прш = Псрш, можно запи- сать РпорТПсршШо. Из этого выражения можно сделать вывод, что пороговая чувствительность СР такого же порядка, как у супергетеродина с коэффициентом шума Шо при условии, что шумовая полоса последнего равна шумовой полосе СР. Таким образом, коэффициент р можно рассматривать в соответствии с (4.5) либо как коэффициент увеличения коэффициента шума, либо в соответствии с (4.8) как коэффициент увеличения полосы при неизменном коэффициенте шума. Эквивалентная шумовая температура СР Тш сррТш) где 7ш - шумовая температура приемника с постоянными параметрами. - иг Рис. 4.3. Увеличение коэффициента шума в СР по сравнению с усилителем с постоянными параметрами (р) в зависимости от аргумента функции Бесселя (при постоянных Q и Y - от глубины суперизации п) 4.2. Сигнал и шум на выходе детектора после сверхрегенератора До сих пор рассматривалось отдельно воздействие детерминированного сигнала и стационарного шума. Между тем сигнал и шум воздействуют на СР одновре- 9-3108 J29 менно. Для CP в линейном режиме такое независимое рассмотрение справедливо в силу действия принципа суперпозиции. Для нелинейного режима необходим другой подход. Кроме того, следует учесть влияние детектора, включенного после CP, так как в детекторе про-
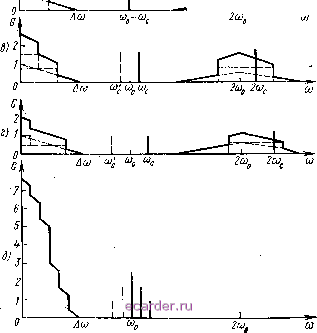 Рис. 4.4. Спектральное распределение шума на выходе квадратичного детектора при совместном действии шума и немодулированной несущей на входе CP:. а -частотная характеристика К((й) и спектр сигнала на выходе CP S(to), т. е. на входе детектора; б, в, г - спектры шума при поступлении сигнала иа частотах (Оо, Cuo+23tF и Сио+4л соответственно; д - спектр низкочасТчтной области шума при поступлении сигнала с указанным на рисунке спектром. Отпо-шепие сигнал-шум = 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 [42] 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||