Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 [44] 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

г]эафиков на рис. 4.5 и 4.6 показывает, что при одних и тех же значениях q к р отношение сигнал-шум на выходе линейного детектора выше, чем у квадратичного.

Рассмотрим роль инерционности нагрузки. Если нагрузка инерционна и время усреднения результатов наблюдения равно Т, интенсивность флуктуации должна вычисляться не по формуле (4.11), справедливой лишь для безынерционного детектора, а по формуле

2 Г/ x \

\\~j{)ck, (4.15)

где Ч(т) - корреляционная функция процесса на выходе детектора,

для низкочастотных составляющих па выходе кв;1дратнчногп детектора ее вычисляют по формуле

¥(т)=<г{л2(т-2?V(t))], (4.16)

где г(х) - нормированная корреляционная функция узкополоеного случайного процесса а входе детектора, зависящая от вида избирательной системы.

Подставляя (4.16) в (4.15) и интегрируя, найдем интенсивность шума, которую надлежит поставить в знаменатель формулы (4.13)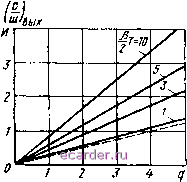

Рис. 4.7. Зависимость отношения сигнал-шум на выходе квадратичного детектора от отношения сигнал-шум на входе при ипсрционпон нагрузке

для определения отношения сигнал-шум на выходе квадра-тичного детектора при инерционной нагрузке. Заменяя q на qp в формуле (4.16), подставляя затем (4.16) в (4.15) и выполняя интегрирование, получаем выражение для шума, которое следует подставить в знаменатель формулы (4.14) для определения отношения сигнал-шум на выходе квадратичного детектора, включенного после CP при иперциониой нагрузке. По результатам этих вычислений построены кривые, представленные на рис. 4.7. Из сопоставления кривых на рис. 4.5 и 4.7 видно, что с увеличением Т отношение сигнал-шум на выходе возрастает по сравнению с безынерционной нагрузкой (штриховая кривая), однако это увеличение будет тем менее значительным, чем глубже суперизация.

Таким образом, можно сделать следующие выводы:

отнощение сигнал-щум иа выходе линейного и квадратичного детекторов, включенных после СР, будет меньше, чем на выходе детекторов, включенных после обычного приемника;

степень ухудшения отношения сигнал-шум на выходе возрастает с глубиной суперизации и обычно составляет несколько единиц;

с увеличением инерционности нагрузки детектора отношение сигнал-шум на выходе возрастает, но тем в меньшей степени, чем глубл<е суперизация, однако увеличение Т ограничивает длительность импульса, которая должна быть соизмерима с 0;

При прочих равных условиях (одинаковых q и Т) линейный детектор на выходе СР даст лучшее отношение сигнал-шум на выходе, чем квадратичный.

Если на вхоДе СР действует модулированное частотой Fm колебание, под сигналом на выходе детектора нужно понимать низкочастотное напряжение с амплитудой t/max- Тогда, кзк показано в [35], отношение сигнал-шум на выходе УНЧ после квадратичного или линейного детектора будет в Vр раз хуже, чем у супергетеродина:

(с/ш) , VJKF (mqlV). (4-17)

где Пт - шумовая полоса до детектора; AF-полоса пропускания после детектора; q=clm на входе детектора. При весьма вероятных значениях Пш=2ЛР и як0,7 выражение (4.17) .превращается в (4.13). Таким образам, кривые для р=1 на рис. 4.5 и 4.6 можно рассматривать как соответствующие AM сигналу для супергетеродина. Легко показать, что и выражение (4.14) характеризует Ьтношение сигнал-шум на выходе СР при модулированном сигнале.

Отсюда можно сделать вывод, что все результаты, полученные выше, в частности графики иа рнс. 4.5, и 4.6, справедливы не только для импульсных сигналов, но и для AM сигналов при сделанных выше оговорках. Следовательно, отношение сигнал-шум на выходе детектора для амплитудно-модулированных или амплитудно-манипулированных (импульсных) сигналов меньше, чем аналогичное отношение для супергетеродина в V р раз. Например, в типовом стабильном режиме при аргументе

функции Бесселя р=5 ... 6 это ухудшение, как видно из рис. 4.3, равно примерно двум.

Рассмотрим статистические характеристики смеси сигнала и шума на выходе детектора, включенного после СР. При поступлении на вхд CP гармонического сигнала без шума спектр выходного напряжения линей-

									. Спектр сигнала u(f)
		\ \ \				\ \ \				\ Энергетический \спек1пр шума s(f)

Рис. 4.8. Спектр колебаний на пыходе детектора для:

о - не.моду.пированного cHni.uia; б - модулированного; о - смеси спшала и шума

чатый. После детектирования такого сигнала получаем напряжение, спектр которого представлен на рис. 4.8,а. Если входной сигнал был модулирован частотой Fm, то вокруг частотных компонентов, отстоящих друг от друга на F, появятся боковые частоты, сдвинутые относительно kF на ±fm (рис. 4.8,6).

Если на вход приемника поступает слабый сигнал, соизмеримый с шумом, вместо последовательности импульсов одинакового уровня при немодулированном сигнале получим серию импульсов одинаковой формы, но

				1 Л ,

Рис. 4.9. Последовательность продетектированных импульсов после детектора

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 [44] 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82