Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 [48] 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

Storo резистора колебания срываются. Замена резистора модулятором Т2, на базу которого поданы импульсы суперизации, переводит каскад в режим сверхрегенерации с малым уровнем ударных колебаний.

На радиочастотах в качестве параметрических рези-стивных элементов удобнее всего использовать модуляторы на биполярных или полевых транзисторах. Однако эти модуляторы не обеспечивают полной развязки CP и источника импульсов суперизации, так как на выходе

Вход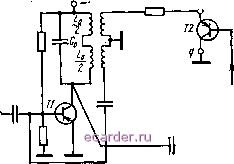

Суперищия

Выход

Рис. 4.14, Сверхрегенератор с безударной суперизацией

модуляторов наблюдаются остаточные напряжения и протекают импульсы тока во время переходных процессов. Кроме того, возможно проникновение импульсов суперизации в схему CP через обслуживающие цепи, например через цепи питания. Поэтому на практике потенциальные возможности CP по чувствительности реализуют за счет развязки и одновременного уменьшения крутизны импульсов суперизации. При этом ударные колебания не проявляются уже при Y = fс о<0,01.

4.6. Ударные колебания и пяроговая чувствительность параметрических сверхрегенераторов

В параметрических (2.27), (2.40) и (2.41), ческих воздействия - с той накачки. При этом с уравнением (2.27) на коэффициент при dxidt,

CP, описываемых уравнениями осуществляются два параметри-частотой суперизации и с часто-в емкостном CP в соответствии частоте суперизации изменяется а на частоте накачки - коэффи-

циент при X, в индуктивном СР в соответствии с уравнением (2.40) на частоте суперизации изменяется коэффициент при dzldt, а на частоте накачки - коэффициент при Z. В обоих случаях на частоте суперизации изменениям подвергается активное сопротивление, а на частоте накачки - энергоемкие элементы (индуктивности или емкости). В резистивном СР, который описывается уравнением (2.41), одновременно с частотами накачки и суперизации изменяется знакопеременное активное сопротивление. В схемах с модуляцией накачки реализуется лишь одно параметрическое воздействие -на частоте накачки, однако с изменяющейся амплитудой.

Если параметрические воздействия заменяются силовыми (электрическими) воздействиями на нелинейные элементы, которые тем или иным образом включены в схемы СР, то наблюдаются два эффекта: изменение необходимых параметров (полезный эффект) и переходные процессы на собственной частоте системы, обусловленные прямым действием на контур СР напряжений (токов) накачки и суперизации (паразитный эффект). Паразитные переходные процессы, называемые ударными колебаниями, впервые описаны в [28, 89].

Попытаемся выяснит., как нелинейные суперизация и накачка вызывают паразитные колебания, после чего определим пороговую чувствительность параметрических СР при наличии этих колебаний и обсудим методы ее повышения. Анализ показывает, что характер ударных колебаний во всех параметрических СР в основном одинаков. Поэтому имеет смысл рассмотреть эти колебания лишь в одном, например, резистивном СР. Предположим, что требуется реализовать резистивный СР, которая описывается уравнением (2.41). Для этого необходимо построить контур, содержащий индуктивность Lo, емкость Со, источник некоторого внешнего воздействия e{t) и знакопеременное активное сопротивление, изменяющееся по закону R{t)-Ro(t)+Яшах cos 2vt, где Ro(t)~ резистор, меняющийся с частотой суперизации. Обсудим три реализации подобного контура.

Первый вариант. Считаем, что каким-либо образом удалось воспроизвести параметрическое воздействие на частоте накачки, т. е. реализовать без сопутствующих эффектов сопротивление Rs(t)=RmaxCos2vt. Что же касается резистора Ro{t), то его реализацию будем связывать с использованием нелинейного элемента (НЭ) 10* 147

с вольт-амперной характеристикой u=f{i). Включим этот элемент вместе с источниками тока суперизации l{t) и полезного сигнала e{t) в контур СР. В итоге получим схему, показанную на рис. 4.15,а.

Полагая, что ток суперизации протекает только по нелинейному элементу, его вместе с источником l{t) в линейном приближении заменяем последовательно

включенными резистором -/?о(0= dT {/[(ОЛ и источником напряжения Е{t)=f [1 {t)]. В результатеприходим к эквивалентной схеме, изображенной на рис. 4.15,6.

0 . х

L ИЗ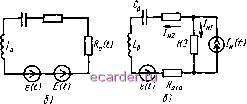

Рис. 4.15. Эквивалентные схемы резистивного параметрического CP с нелинейными элементами в цепях суп§рнзации и накачки

В этой схеме г{1)=-е(t)-Е{t), т. е. наряду с полезным сигналом е(0 присутствуют видеоимпульсы E(t), вызывающие ударные колебания.

Эффект чистых ударных колебаний можно описать с помощью уравнения (2.41), если положить, что е(0 = E(t). Решение этого уравнения имеет вид (2.39).

Пусть осуществляется однократный запуск CP, когда на схему подан один импульс E{t). Запишем этот импульс в форме E{t)-EmaxHy{t), где fmax -амплитуда импульса; Яy(i) - нормированная безразмерная функция. Подставив данный импульс в выражение (2.39), получим выходной процесс СР.

(4.29)

(О = --БшахЛО vlKe cos (V - cpj X

Обозначим далее через Hia{t) произведение Hi{t)Hy{t) и воспользуемся спектральной функцией 5ia(jA©), найденной по формуле (3.1) при подстановке в нее вместо i,2(0 зависимости Hlt). После неслож-148

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 [48] 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82