
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 [76] 77 78 79 80 81 82 ния колебаний) резистором R. Сигнал вводится из антенны в катушку связи Lcb, связанную с L. Между эмиттером и коллектором включен накопительный конденсатор Сн, заряжающийся от источника через резистор /?ф. Дроссель Др изолирует коллектор от Сц по высокой частоте. При включении источника напряжение на Сд равно нулю, колебаний нет и начинается заряд Сн через сопротивление Яф. Когда напряжение на Сн достигнет уровня, достаточного для возникновения колебаний, контур начнет генерировать. При этом конденсатор Сн раз- 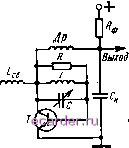 Рис. 6.24. Частотная характеристика CP в когерентном режиме (/) я линия обратной связи ( ) Рис. 6.25. Принципиальная схема высокоэкономичного и стабильного CP на СВЧ ряжается через открытый транзистор, что вскоре приводит к срыву колебаний. Затем процесс повторяется. Из-за низкого сопротивления в цепи разряда частота суперизации может быть очень высокой. Напряжение суперизации и продетектированный сигнал выделяются на резисторе Рф. Напряжение суперизации подавляется фильтром низких частот или входным сопротивлением активных фильтров, которые подключаются к точке выход для последующего усиления. Заметим, что особенностью схемы является отсутствие постоянного напряжения на переходе коллектор - база. Несмотря на это, транзистор находится в активном усилительном режиме, поскольку указанный переход смещен в обратном направлении контактной разностью потенциалов. В заключение укажем на основные направления, по которым, на наш взгляд, будут развиваться теория и практика сверхрегенеративных устройств: совершенствование схем CP (расширение ассортимента приборов, создающих эффект отрицательного сопротивления, освоение новых диапазонов частот, снижение уровня собственных шумов, разработка новых методов параметрических суперизации и накачки); повышение отношения сигнал-шум на выходе СР при различных видах помех и сигналов; совершенствование схем обработки сигналов с предварительной фильтрацией (параметрические квантователи фазы, высокоэкономичные приемники сигналов с амплитудной или угловой модуляцией с потреблением тока от десятков до сотен микроампер); разработка локационных и связных систем с оптимальными для СР сигналами (обнаружители, дальномеры, системы связи с импульсной модуляцией); оптимизация сверхрегенеративных устройств для регистрации сигналов ЯМ.Р и ЯКР; разработка новых и улучшение параметров существующих фазовых СР (доплеровские обнаружители СВЧ диапазона); создание теории обработки сигналов в многоконтурных и апериодических СР (последние описываются дифференциальными уравнениями первого порядка); дальнейшее совершенствование конструкций, главным образом разработка конструкций сверхрегенеративных устройств в интегральном исполнении. ПРИЛОЖЕНИЕ. Решение однородного уравнения с переменными коэффициентами При анализе схемы комбинированного параметрического СР использована методика решения линейных дифференциальных уравнений с медленно меняющимися коэффициентами, восходящая к работам щколы И. М. Крылова и Н. Н. Боголюбова. В [38] эти методы применены к уравнениям, содержащим кроме медленно меняющихся коэффициентов, быстро колеблющиеся множители, что сделало возможным решение поставленной задачи. Выразим d, I и m через у. Величины d=ay, £о = Ру ч п=р,у малы по сравнению с единицей. Обозначив yt=x, уравнение (2.43) с учетом (2.42) можно привести к векторно-матрпчной форме о 1 -1 о 5 =
о о -6, -а, д1= - аре * (1-f н cos х); 6,= -/г cost); / О \ Ф(П = I f (О / (П. 2) Рассмотрим сначала однородное уравнение (П.З) соответствующее уравнению (П.1). Его решение можно представить в виде W{t)==U(t, to)Wo, где Wo = w\to), U(t, to) - матричная функция, удовлетворяющая тому же уравнению (П.З) и условию U(t, to)-I. Будем искать эту функцию в виде иа, to, y) = YUt, to. y)U,(t, to, y)+Y~i(t, to, Y)X XU-.i{t, to, Y), (П.4) где функции {t, t , f) имеют вид У = ехр J Qt, Y)rf . s = + 1. a функция Qs и матрица С/*** представимы в виде разложений оо 00 /=0 Коэффициенты Q и (У]* неизвестны, но, подставляя разложения (П.4) в исходное уравнение и приравнивая коэффициенты при членах вида exp[jk2(-to)\Ysy , получаем систему рекуррентных соотношений для них. Эти соотношения можно последовательно решить, выполняя обычные операции над матрицами. Учитывая лишь члены разложения (П.5) не выше первого, можно получить матри- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 [76] 77 78 79 80 81 82 |